Dimensionen der Messung
Skalenniveau
1) Ordinalskala
2) Nominalskala
3) Intervallskala
4) Verhältnisskala
Literatur
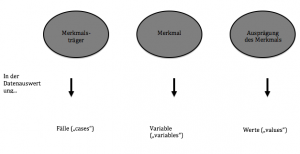
Es gibt verschiedene Dimensionen der Messung, die in der Planungsphase einer Studie zu beachten sind. In der wissenschaftlichen Vorbereitung spricht man von einer „Untersuchungseinheit“, also dem Merkmalsträger, welcher hinsichtlich verschiedener „Merkmalen“ und deren „Ausprägung“ untersucht wird.
Übersetzt in unsere Alltagssprache ist die Untersuchungseinheit ein zuvor ausgewähltes Objekt, welches beobachtet, befragt oder inhaltsanalytisch untersucht werden soll. Das Merkmal bezieht sich auf die untersuchungsrelevanten Eigenschaften, die das Objekt besitzt. Mit der Ausprägung des Merkmals ist eine ganz bestimmte Variante der Eigenschaft gemeint.
An einem Beispiel lassen sich die drei Dimensionen verdeutlichen.
| Haarfarbe | Bildungsabschluss | |
| Luca | blond | Realschulabschluss |
| André | braun | Abitur |
| Lisa | schwarz | Hauptschulabschluss |
Die drei Personen Luca, André und Lisa stellen die Untersuchungseinheiten (Objekte) dar. Die Haarfarbe und der Bildungsabschluss sind zwei Merkmale (Eigenschaften). Die beiden Merkmale haben bei den unterschiedlichen Personen jeweils verschiedene Ausprägungen (Variante der Eigenschaft). Die Haarfarbe hat die Ausprägungen „blond“, „braun“ und „schwarz“. Der Bildungsabschluss differenziert sich in die Ausprägungen „Realschulabschluss“, „Abitur“ und „Hauptschulabschluss“.
Am Ende einer Untersuchung, in der Datenauswertung, spricht man von den Merkmalsträgern als „Fälle“ (cases). Die Merkmale werden „Variablen“ (variables) genannt und unter „Werten“ (values) versteht man die Ausprägungen des Merkmals.
Mit dem Skalenniveau wird die mathematische Qualität einer Merkmalsausprägung beschrieben. Das jeweilige Skalenniveau drückt aus, wie präzise das empirische Relativ erfasst wird. Die Festlegung des Skalenniveaus entscheidet auch darüber, welche Rechenoperationen im Rahmen der Auswertung angewendet werden können. Je nach Art der erhobenen Merkmale kommen verschiedene Skalen zur Anwendung. Es gibt „grobe“ Skalen, die von Natur aus nur wenige Antwortmöglichkeiten (Augenfarbe: blau, grün oder braun) erlauben und „detailliertere“ mit vielen potentiellen Antwortmöglichkeiten (Größe: 1,50m; 1,51m; … 2,00m, 2,01m). Je nachdem, wie die jeweilige Variable skaliert ist, sind unterschiedliche Interpretationen möglich. Generell sind Ausprägungen von Merkmalen in folgende vier Skalen zu unterteilen:
| Skalenniveau | Aussagen zu Messwerten | Nullpunkt | Rechenoperatoren | Beispiel |
| Nominalskala | Gleichheit/Ungleichheit | nein | A=B=C …oder A≠B≠C… | Telefonnummern,Geschlecht |
| Ordinalskala | Rangreihe | nein | A <B <C… oder A> B> C… | Energieeffizienzklassen, Fahrzeugklassen |
| Metrisch: Intervallskala | Gleiche Abstände zwischen den Rängen | nein | B-A=C-B=D-C | IQ-Skala, Temperatur in Celsius |
| Metrisch: Verhältnisskala | Gleichheit von Verhältnissen | ja | A÷B=B÷C=C÷D | Länge, Gewicht |
(1) Nominalskala: Die Nominalskala entspricht dem niedrigsten Messniveau. Bei ihrer Interpretation kann man nicht sagen, dass die eine Merkmalsausprägung besser oder schlechter als eine andere ist. Diese Skala bildet nur die Gleichheit oder Ungleichheit ab. Das Merkmal muss mindestens zwei Ausprägungen haben, beispielsweise ob ein Merkmal „vorhanden“ oder „nicht vorhanden“ ist. Deutlich wird an diesem Beispiel das niedrige Messniveau; man kann nicht sagen, grüne Augen seien besser oder schlechter als blaue Augen.
Man unterscheidet in dichotome und polytome Variablen. Wie es der Wortanfang bereits verrät, handelt es sich bei „di“-chotomen Variablen um solche, die nur zwei Ausprägungen haben. Ein Beispiel dafür ist die Frage nach dem Geschlecht, diese wird entweder mit männlich oder weiblich beantwortet. Bei einer „poly“-tomen Variablen handelt es sich um solche, die mehrere Ausprägungen haben.
(2) Ordinalskala: Diese Skala bildet eine Rangreihe ab, man kann die Messwerte also in Ränge unterteilen bzw. in eine Rangfolge bringen und somit in „besser“ und „schlechter“ oder „größer“ und „kleiner“ unterscheiden. Ein Beispiel für eine Ordinalskala kann aus der soziologischen Schichtentheorie abgeleitet werden, denn auch wenn die bestehende Einteilung in Oberschicht, Mittelschicht und Unterschicht nicht mehr ganz zeitgemäß ist, so symbolisieren die Schichten der Gesellschaft doch statistisch eine hierarchisch geordnete Rangfolge. Achtung: Die Abstände zwischen benachbarten Rängen sind nicht gleich!
Achtung: Ab hier beginnt das metrische Messniveau!
(3) Intervallskala: Bei der Intervallskala sind zusätzlich die Abstände zwischen den Merkmalsausprägungen gleich groß. Zu dieser Skala zählt beispielsweise die Messung von Temperatur in Celsius, da die Einheiten des Thermometers immer exakt ein Grad betragen, allerdings kennt diese Skala keinen absoluten Nullpunkt. Das bedeutet, dass die Temperaturangabe auch negative Werte annehmen kann.
(4) Verhältnisskala: Bei der Verhältnis- bzw. Ratioskala sind sowohl die Abstände als auch die Verhältnisse zwischen den benachbarten Merkmalsausprägungen gleich. Außerdem gibt es hier einen absoluten bzw. natürlichen Nullpunkt. Als Beispiel kann die Frage nach dem Alter dienen, da es in diesem Fall mit der Geburt einen eindeutigen Nullpunkt gibt. Die Abstände von Lebensjahr zu Lebensjahr betragen immer 365 Tage, wodurch die Verhältnisse zwischen den Datenpunkten identisch sind.
Lohninger, Hans (2012): Sohlenniveau. Zugriff am 20.02.2017.
MatheGuru (2011-2017): Skalen, Skalenniveaus. Zugriff am 20.02.2017.
Scheufele, Betram/Engelmann, Ines (2009): Empirische Kommunikationsforschung. Konstanz: UVK-Verl.-Ges., S. 49-53.
Statista: Statistik-Lexikon: Definition Skalenniveau. Zugriff am 20.02.2017.