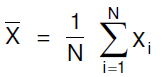Modus/Modalwert | Arithmetisches Mittel/Mittelwert | Median/Zentralwert
„Parameter oder Kennwerte einer Häufigkeitsverteilung sind Kenngrößen, mit deren Hilfe die Verteilung z.T. oder vollständig rekonstruiert werden kann“ (Müller-Benedict 2011: 64).
Die Lageparameter beschreiben zentrale Punkte einer Häufigkeitsverteilung. Die geläufigsten sind der Modus, der Median, der Mittelwert und die Standardabweichung.
„Der Modus oder Modalwert D einer kategorialen Häufigkeitsverteilung ist der Wert der häufigsten Merkmalsausprägung. Sind mehrere Ausprägungen gleich häufig, so gibt es mehrere Modalwerte“ (Müller-Benedict 2011: 65).
Bei unserem Beispiel der Schulnoten müssen wir die Note mit der häufigsten Ausprägung suchen.
| Note | absolute Häufigkeit |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 3 |
| 5 | 3 |
| 6 | 2 |
| Σ | 20 |
Da die Note 3 mit einer absoluten Häufigkeit von 6 die häufigste Ausprägung besitzt, ist sie der Modalwert.
Vorsicht: Der Modus ist nur bei ordinalskalierten Daten anwendbar!
Vorteil: Der Modus ist robust gegenüber Ausreißern!
Arithmetisches Mittel/Mittelwert
„Der Mittelwert oder das arithmetische Mittel eines Merkmals X wird wie folgt gebildet. Sei N = Anzahl der Fälle und xi die Ausprägung des i-ten Falls. Dann ist
In unserem Beispiel der Schulnoten wird der Mittelwert der Noten anhand der Formel wie folgt berechnet:
(1+1+2+2+2+2+3+3+3+3+3+3+4+4+4+5+5+5+6+6):20=3,35 bzw.
(1*2+2*4+3*6+4*3+5*3+6*2):20=3,35 direkt anhand obiger Tabelle.
Vorsicht: Der Mittelwert ist nicht robust gegenüber Ausreißern!
„Der Median oder Zentralwert (Z) eines Merkmals ist die Ausprägung des Falls in der Mitte der der Größe nach (man sagt auch: nach Rangplätzen) geordneten Fälle. Bei einer geraden Anzahl wird die Ausprägung der beiden in der Mitte liegenden Fälle gemittelt“ (Müller-Benedict 2011: 67).
Bei ungerader Anzahl rechnet man (Gesamtzahl der absoluten Häufigkeiten +1):2.
In unserem Beispiel der Schulnoten müssen die Noten zunächst nach Rangplätzen geordnet werden:
| Note | absolute Häufigkeit |
| 3 | 6 |
| 2 | 4 |
| 4 | 3 |
| 5 | 3 |
| 6 | 2 |
| 1 | 2 |
| Σ | 20 |
Mit 20 haben wir eine gerade Anzahl an Fällen. Somit muss der Mittelwert des 10. und 11. Platzes ( = in der Mitte liegende Fälle) berechnet werden. Der 10. Platz ist die Note 2. Der 11. Platz die Note 4.
Somit ergibt sich ein Median von (2+4):2=3