Grundlagen | Schritte eines Signifikanztests | Chi‐Quadrat nach Pearson | Interpretation der Kreuztabelle
Ein statistischer Test entscheidet anhand von Stichprobenergebnissen, ob eine statistische Hypothese vorläufig akzeptiert werden kann oder verworfen werden muss. Das passiert mit einer bestimmten Fehlerwahrscheinlichkeit.
In der Regel werden die Tests in Form von Signifikanztests durchgeführt.
- H1 = Alternativhypothese („Was ich zeigen oder beweisen will“)
- H0 = Nullhypothese („Alles bleibt beim Alten“)
Irrtumswahrscheinlichkeit p = Signifikanzniveau
→ Wahrscheinlichkeit, dass ich einen Fehler begehe, wenn ich das Ergebnis für die Grundgesamtheit annehme
- p ≤ 0,05 : Stichprobenergebnis „statistisch signifikant“
- p ≤ 0,01 : sehr signifikant/hoch signifikant
- p ≤ 0,001 : höchst signifikant
Entspricht jeweils einer Irrtumswahrscheinlichkeit von 5% bzw. 1% bzw. 0,1%.
Schritte eines Signifikanztests
- Formulierung der Nullhypothese H0 und der Alternativhypothese H1
- Festlegung des Signifikanzniveaus
- Bestimmung des Annahme- und Ablehnungsbereichs der H0
- Ziehung der Stichprobe und Durchführung des Tests
- Treffen der Testentscheidung und Interpretation
→ Liegt das Ergebnis der Stichprobe innerhalb des Annahmebereichs, wird H0 angenommen, andernfalls abgelehnt
Die Annahme der H0 führt zur Ablehnung der H1, ist aber kein Beweis dafür, dass H0 stimmt.
Chi‐Quadrat nach Pearson: Unabhängigkeitstest
Der Chi‐Quadrat‐Test untersucht stets die Hypothese: Es besteht kein Zusammenhang zwischen den untersuchten Variablen.
Im Beispiel der Schulklasse und ihren Noten können wir nun einen Schritt weiter gehen und über mehrere Schulklassen überprüfen, ob Geschlecht und Note zusammenhängen. Solche Tendenzen lassen sich in der Kreuztabelle ablesen.
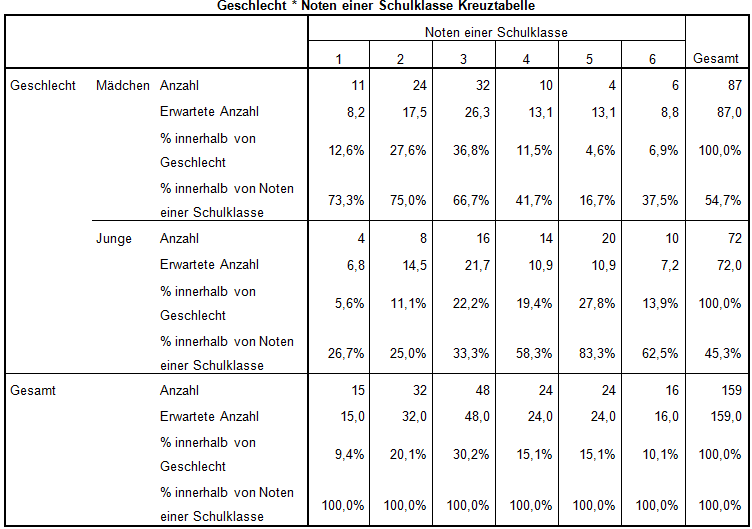
Tabelle 1
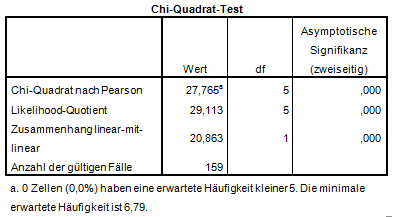
Tabelle 2
Derartige statistische Berechnungen können mit einem computergestützten Programm (z. B. SPSS) durchgeführt werden.
Die genauen Analyseschritte werden im Folgenden vorgestellt.
Die Interpretation der Kreuztabelle und Test in vier Schritten
(1) Welche zwei Variablen werden auf Unabhängigkeit geprüft?
(2) Betrachtung der Prozentwerte. Wie kann man die Ergebnisse in den einzelnen Zellen interpretieren? Wo sind starke Abweichungen zu erkennen und warum? (Formulieren im Konjunktiv)
(3) Erste Zeile unter der Testtabelle: Überprüfe den Prozentsatz der Zellen mit einer erwarteten Häufigkeit kleiner als 5 → bis 20% in Ordnung (=gültig); andernfalls hat der χ2-Test keine Aussage mehr, da man dann mit zu wenigen Fällen rechnet.
Falls der Test gültig ist: Ist das Testergebnis (zweiseitige Signifikanz) signifikant (max. 5% Irrtumswahrscheinlichkeit)?
(4) Schlussfolgerung/Ergebnis: Sind die Variablen unabhängig und könnten die beobachteten Abweichungen auch auf einem Zufall beruhen (nicht signifikant) oder besteht ein signifikanter Zusammenhang zwischen den Variablen und die Nullhypothese muss verworfen werden?
In unserem Notenbeispiel:
(1) Wir testen die Abhängigkeit der Variablen Noten und Geschlecht.
(2) In Tabelle 1 kann man die Häufigkeit der jeweiligen Note bei Jungen und Mädchen herauslesen. Fast drei Viertel (73,3%) der Note 1 haben Mädchen (26,7 % Jungen). 37,5 % der Note 6 sind auf Mädchen (62,5% auf Jungen) zurückzuführen. Bei den anderen Noten lässt sich die gleiche Tendenz ablesen. Zudem liegt z. B. die Häufigkeit der guten Noten 1-3 bei den Mädchen stets über der (bei gleichmäßiger Verteilung) erwarteten Häufigkeit (z. B. Note 1: Anzahl 11, bei einer erwarteten Anzahl von nur 8,2). Bei den Jungen verhält es sich umgekehrt. Es scheint, dass Mädchen bessere Noten haben als Jungen.
(3) Man betrachtet zunächst die Fußzeile der Tabelle 2: 0 Zellen (,0%) haben eine erwartete Häufigkeit kleiner 5. Die minimale erwartete Häufigkeit ist 6,79. Der Test ist somit gültig.
Der Wert bei ‘Asymptotische Signifikanz (2-seitig)’ in der Zeile ‘Chi-Quadrat nach Pearson’ zeigt das Signifikanzniveau an. Der Wert 0.00 weist – wie oben beschrieben – darauf hin, dass der Zusammenhang höchst signifikant ist.
(4) Nun wissen wir, dass zwischen der Note und dem Geschlecht ein höchst signifikant nachgewiesener Zusammenhang besteht; die Nullhypothese muss verworfen werden.
Vorsicht: Dies weist weder auf eine Kausalität hin, noch kann gesagt werden, ob der Zusammenhang stark oder schwach ist. Dazu benötigt man Korrelationen.
Informationen zu Korrelationen lassen sich z. B. hier nachlesen.